
Reconstructing unmeasured causal drivers of complex time series from observed response data represents a fundamental challenge across diverse scientific domains. Latent variables, including genetic regulators or environmental factors, are essential to determining a system’s dynamics but are rarely measured. Challenges with current approaches arise from data noise, the systems’ high dimensionality, and existing algorithms’ capacities in handling nonlinear interactions. This will greatly help in modeling, predicting, and controlling high-dimensional systems in systems biology, ecology, and fluid dynamics.
The most widely used techniques for causal driver reconstruction usually rely on signal processing or machine learning frameworks. Some common ones include mutual information methods, neural network applications, and dynamic attractor reconstruction. While these techniques work well in some situations, they have significant limitations. Most demand large, high-quality datasets that are rarely found in real-world applications. They are very prone to measurement noise, resulting in low reconstruction accuracy. Some require computationally expensive algorithms and thus not suited for real-time applications. In addition, many models lack physical principles, reducing their interpretability and applicability across domains.
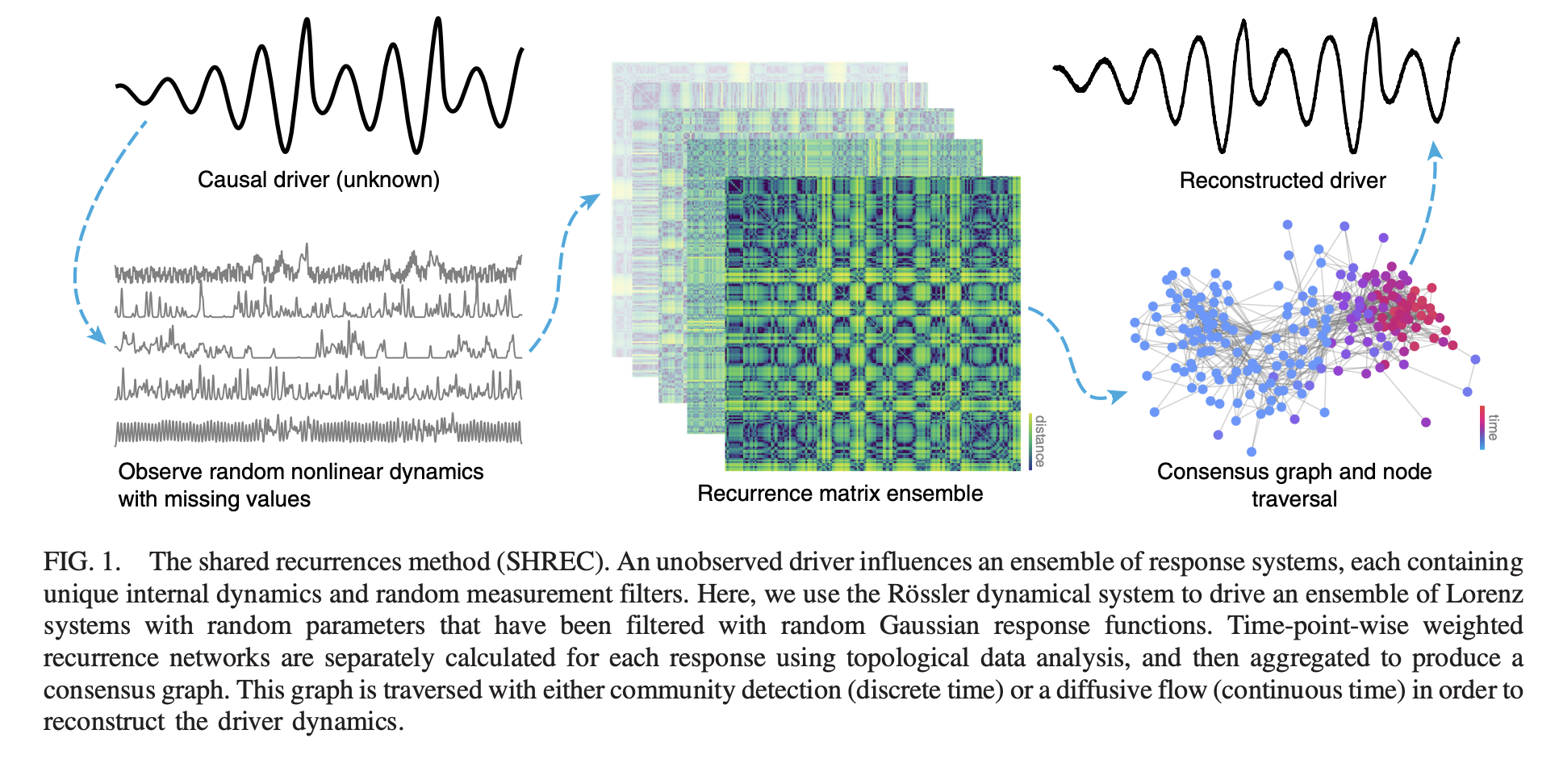
The researchers from The University of Texas introduce a physics-based unsupervised learning framework called SHREC (Shared Recurrences) to reconstruct causal drivers from time series data. The approach is based on the theory of skew-product dynamical systems and topological data analysis. Innovation includes the use of recurrence events in time series to infer common causal structures between responses, the construction of a consensus recurrence graph that is traversed to expose the dynamics of the latent driver, and the introduction of a new network embedding that adapts to noisy and sparse datasets using fuzzy simplicial complexes. Unlike the existing methods, the SHREC framework well captures noisy and nonlinear data, requires minimal parameter tuning, and provides useful insight into the physical dynamics underlying driver-response systems.
The SHREC algorithm is implemented in multiple stages. The measured response time series are mapped into weighted recurrence networks by topological embeddings, where an affinity matrix is constructed for each time series based on nearest neighbor distances and adaptive thresholds. The recurrence graphs are combined from individual time series to obtain a consensus graph that captures collective dynamics. Discrete-time drivers have been linked to decomposition by community detection algorithms, including the Leiden method, to provide distinct equivalence classes. For continuous drivers, on the other hand, the graph’s Laplacian decomposition reveals transient modes corresponding to states of drivers. The algorithm was tested on diverse data: gene expression, plankton abundances, and turbulent flows. It showed excellent reconstruction of drivers under challenging conditions like high noise and missing data. The structure of the framework is based on graph-based representations. Therefore, it avoids costly iterative gradient-based optimization and makes it computationally efficient.
SHREC performed notably well and consistently on the benchmark-challenging datasets. The methodology successfully reconstructed causal determinants from gene expression datasets, thereby uncovering essential regulatory components, even in the presence of sparse and noisy data. In experiments involving turbulent flow, this approach successfully detected sinusoidal forcing factors, demonstrating superiority over traditional signal processing techniques. Regarding ecological datasets, SHREC revealed temperature-induced trends in plankton populations, notwithstanding considerable missing information, thus illustrating its resilience to incomplete and noisy data. The comparison with other approaches has highlighted SHREC’s increased accuracy and efficiency in computation, especially in the presence of higher noise levels and complex nonlinear dependencies. These findings highlight its extensive applicability and reliability in many fields.
SHREC is a physics-based unsupervised learning framework that enables the reconstruction of unobserved causal drivers from complex time series data. This new approach deals with the severe drawbacks of contemporary techniques, which include noise susceptibility and high computational cost, by using recurrence structures and topological embeddings. The successful workability of SHREC on diverse datasets underlines its wide-ranging applicability with the ability to improve AI-based modeling in biology, physics, and engineering disciplines. This methodology improves the accuracy of causal driver reconstruction and, at the same time, puts in place a framework based on the principles of dynamical systems theory and sheds new light on essential characteristics of information transfer within interconnected systems.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. Don’t Forget to join our 65k+ ML SubReddit.
The post SHREC: A Physics-Based Machine Learning Approach to Time Series Analysis appeared first on MarkTechPost.