Large Language Models (LLMs) based on Transformer architectures have revolutionized AI development. However, the complexity of their training process remains poorly understood. A significant challenge in this domain is the inconsistency in optimizer performance. While the Adam optimizer has become the standard for training Transformers, stochastic gradient descent with momentum (SGD), which is highly effective for convolutional neural networks (CNNs), performs worse on Transformer models. This performance gap poses a challenge for researchers. Solving this mystery could improve the theoretical grasp of Transformer training and neural networks, potentially leading to more efficient training methods.
Existing research includes several hypotheses to explain the poor performance of SGD on Transformers compared to Adam. One theory suggests that SGD struggles with heavy-tailed stochastic noise in language tasks. Efforts to understand Adam’s effectiveness have led to convergence analyses for various adaptive gradient methods. Recent studies have explored Hessian spectrum analysis for MLPs and CNNs, identifying characteristic “bulk” and “outlier” patterns. Transformer training difficulties have been attributed to various phenomena, including logits divergence, rank degeneracy in attention layers, parameter norm growth, over-reliance on residue branches, and negative impacts of layer normalization.
Researchers from The Chinese University of Hong Kong, Shenzhen, China, and Shenzhen Research Institute of Big Data explained the performance disparity between SGD and Adam in training Transformers. Their approach focuses on analyzing the Hessian spectrum of these models and the concept of “block heterogeneity,” which refers to the significant variation in Hessian spectra across different parameter blocks in Transformers. Moreover, a hypothesis is presented that this heterogeneity is a key factor in SGD’s underperformance. The experimental results on various neural network architectures and quadratic problems show that SGD’s performance is comparable to Adam’s in problems without block heterogeneity but deteriorates when heterogeneity is present.
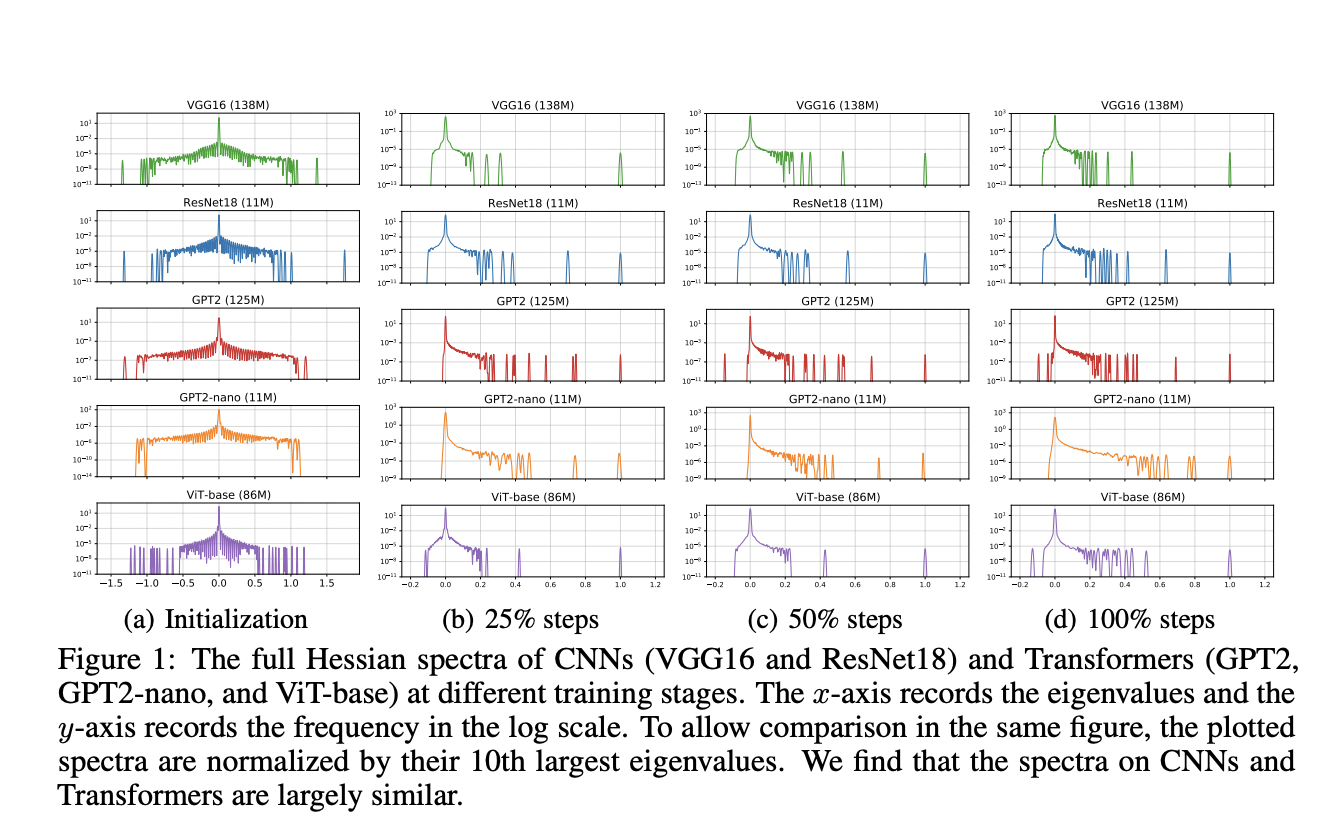
The proposed method utilizes the Stochastic Lanczos Quadrature (SLQ) method to approximate the Hessian spectrum of large-scale neural networks, which are otherwise too complex to compute and store. SLQ approximates the eigenvalue histograms using smooth curves, and this technique is applied to analyze various models, including CNNs (ResNet18 and VGG16) and Transformers (GPT2, ViT-base, BERT, and GPT2-nano) across different tasks and modalities. The full Hessian spectrum and the blockwise Hessian spectrum are evaluated for each model. The parameter blocks were split according to the default partition in PyTorch implementation, such as the Embedding layer, Query, Key, and Value in the attention layers.
The results show a contrast in the Hessian spectra between Transformer models and CNNs. In Transformers like BERT, the Hessian spectra exhibit significant variations across different parameter blocks, such as embedding, attention, and MLP layers. This phenomenon, termed “block heterogeneity,” is consistently observed across all examined Transformer models. On the other hand, CNNs like VGG16 display “block homogeneity,” with similar Hessian spectra across convolutional layers. These differences are quantified using the Jensen-Shannon distance between eigenvalue densities of block pairs. This block heterogeneity in Transformers correlates strongly with the performance gap between SGD and Adam optimizers.
In this paper, researchers explored the underlying reasons for SGD’s underperformance compared to Adam in training Transformer models. The concept of “block heterogeneity” in the Hessian spectrum is introduced, and a strong correlation is established between this phenomenon and the performance gap between Adam and SGD. The study provides convincing evidence that “block heterogeneity”, prevalent in Transformers but not in CNNs, significantly impacts optimizer performance. Moreover, SGD’s performance is not good in the presence of “block heterogeneity”, while Adam remains effective. This work offers key insights into the optimization dynamics of neural network architectures and paves the way for more efficient training algorithms for Transformers and heterogeneous models.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter..
Don’t Forget to join our 52k+ ML SubReddit.
We are inviting startups, companies, and research institutions who are working on small language models to participate in this upcoming ‘Small Language Models’ Magazine/Report by Marketchpost.com. This Magazine/Report will be released in late October/early November 2024. Click here to set up a call!
The post Unraveling Transformer Optimization: A Hessian-Based Explanation for Adam’s Superiority over SGD appeared first on MarkTechPost.