Recent research highlights that Transformers, though successful in tasks like arithmetic and algorithms, need help with length generalization, where models handle inputs of unseen lengths. This is crucial for algorithmic tasks such as coding or reasoning, where input length often correlates with problem difficulty. Large language models face this limitation even when scaled due to their fixed depth. Approaches like Chain-of-Thought reasoning and scratchpad methods offer some improvement. A promising solution is the Looped Transformer, which processes inputs iteratively, allowing adaptive steps based on problem complexity and improving length generalization for algorithmic tasks.
Researchers from the University of Wisconsin-Madison, MIT, and UC Berkeley demonstrate that Looped Transformers with adaptive steps improve length generalization for algorithmic tasks. Focusing on functions with iterative solutions using RASP-L operations, they train Looped Transformers without intermediate supervision, relying solely on input, output, and step count. At inference, the model determines the necessary steps to solve a task. Their method shows that Looped Transformers adapt the number of loops during inference, enabling successful length generalization. The study introduces n-RASP-L problems and demonstrates improved performance on tasks like Copy, Parity, and Addition compared to baseline approaches.
The study explores positional embeddings, RNNs, Chomsky Hierarchy, Universal Transformers, input representations, and Chain-of-Thought (CoT) reasoning in length generalization. Positional embeddings enhance Transformers’ generalization ability but are not used in RASP-L operations. Studies show RNNs and Transformers struggle with non-regular tasks, while structured memory aids in context-free generalization. The Looped Transformer adapts the Universal Transformer with step-dependent supervision, improving task generalization. Additionally, CoT reasoning can simplify predictions, but its steps may introduce complexity that hinders generalization. The study also differentiates between next-token prediction (NTP) and full-answer prediction (FAP) methods.
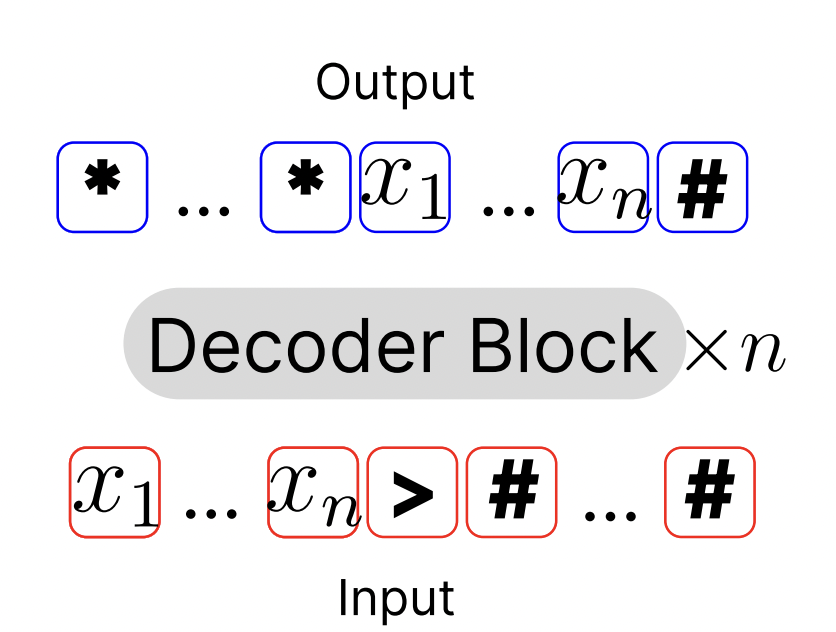
The n-RASP-L framework addresses algorithmic tasks using fixed-depth decoder-only Transformers without loops, making problems like addition or parity challenging. A “looped Transformer” architecture is proposed to solve this, which reuses decoder blocks across multiple iterations based on input length. This allows solving tasks such as n-digit addition and parity through iterative processes. The model is supervised end-to-end during training, using input-output pairs without intermediate steps. At inference, adaptive stopping rules, such as step oracle or confidence thresholds, are employed to decide when to terminate the looped process.
The study assesses the effectiveness of looped Transformers for tasks requiring length generalization. Various tasks were evaluated, including parity, copy, addition, binary sum, and multiplication. The experimental setup involves curriculum learning, and the looped model shows superior generalization, especially in handling longer sequences beyond training lengths. Comparisons with baseline methods like vanilla NTP, NTP with pause tokens, and weight-tied layers show that the looped model with adaptive depth significantly outperforms these approaches. Ablation studies highlight the positive impact of input injection and adaptive depth on performance, with stopping criteria based on maximum confidence ensuring optimal outputs.
This work has several limitations, including the computational demands of direct looped training when handling many steps and limited training data due to resource constraints. Using simpler positional embeddings (NoPE) also leaves room for improvement. Despite requiring ground-truth step numbers for supervision, the method assumes less than CoT training. In conclusion, looped Transformers with step-dependent supervision effectively improve length generalization, particularly for challenging n-RASP-L tasks. While previous models struggled with unseen input lengths, this approach adapts the number of steps during inference, showing potential for broader applications in more complex reasoning tasks.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter..
Don’t Forget to join our 52k+ ML SubReddit.
We are inviting startups, companies, and research institutions who are working on small language models to participate in this upcoming ‘Small Language Models’ Magazine/Report by Marketchpost.com. This Magazine/Report will be released in late October/early November 2024. Click here to set up a call!
The post Improving Length Generalization in Algorithmic Tasks with Looped Transformers: A Study on n-RASP-L Problems appeared first on MarkTechPost.