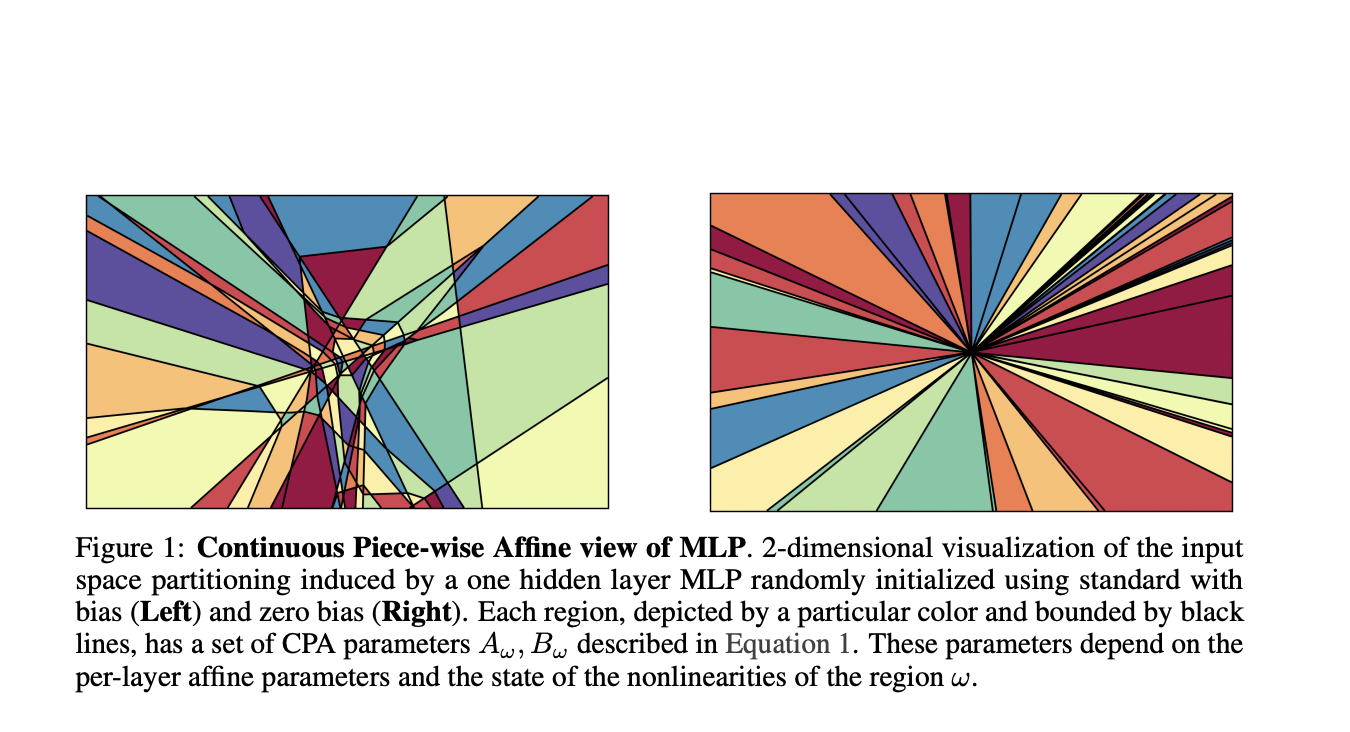
Large language models (LLMs) have demonstrated remarkable performance across various tasks, with reasoning capabilities being a crucial aspect of their development. However, the key elements driving these improvements remain unclear. Currently, the primary approaches to enhance reasoning involve increasing model size and expanding context length through techniques like chain of thought, retrieval augmented generation, and example-based prompting. While effective, these methods represent only a fraction of potential improvement avenues and often lead to increased computational costs and inference latency in real-world applications.
Existing attempts to understand LLMs have approached the problem from various angles. Some researchers have focused on mechanistic frameworks or pattern analysis through empirical results. Others have explored input-output relationships using domain-specific approaches, such as graph problems to assess LLM expressiveness, algorithmic reasoning to understand limitations, and arithmetic learning to investigate the impact of input formatting. Studies on transformers have also examined initialization, training dynamics, and embedding geometry in intermediate and last layers. However, these approaches often lack a comprehensive end-to-end geometric perspective and typically do not account for the sequence dimension or offer a context-dependent analysis of LLMs, particularly in relation to model size, context length, and their roles in reasoning capabilities.
Researchers from Tenyx provide this study to explore the geometry of transformer layers in LLMs, focusing on key properties correlated with their expressive power. The research identifies two critical factors: the density of token interactions in the multi-head attention (MHA) module, which reflects the complexity of function representation achievable by the subsequent multi-layer perceptron (MLP), and the relationship between increased model size and context length with higher attention density and improved reasoning. The analysis investigates how the LLM’s geometry correlates with its reasoning capabilities, particularly examining the impact of increased input sequence length and number of attention heads. By exploring the intrinsic dimension of the self-attention block and analyzing the graph density of each attention head, the study aims to capture the expressive power of LLMs and deepen the understanding of their behavior, potentially opening new avenues for advancing LLM capabilities.
The study analyzes LLMs’ reasoning capabilities through geometric analysis, focusing on how increased regions induced by the Multi-Layer Perceptron affect reasoning. Using the GSM8K-Zero dataset, experiments with question-answer pairs and random tokens reveal that while prepending tokens increases intrinsic dimension at the first layer, improved reasoning correlates with increased intrinsic dimension at the final layer. The last layers’ intrinsic dimension proves highly informative about response correctness across model sizes. These findings demonstrate a correlation between expressive power and reasoning capabilities, suggesting that enhancing input complexity to MLP blocks can improve LLMs’ reasoning performance.
The study reveals a strong correlation between the intrinsic dimension (ID) of the last layers and response correctness, regardless of model size. Experiments show that increasing context in prompts can raise the ID, particularly when the context is relevant to the question. This leads to more piece-wise affine maps in the MLP, resulting in more adaptive transformations for each token. From an approximation standpoint, finer partitioning around tokens reduces overall prediction error. The research demonstrates that higher ID changes correlate with increased probability of correct responses. However, the relationship between these geometric insights and the generalization capabilities of LLMs remains an unexplored area, warranting further investigation to understand the models’ robustness and adaptability across various contexts.
This research highlights the importance of input space partitioning induced by MLPs in DNNs and LLMs. The adaptive partitioning of DNNs plays a crucial role in their approximation capability, with regions in the input space being data-dependent and determined during training. The study demonstrates how the interplay between approximation and the number of regions impacts LLMs’ function approximation abilities. While approximation power is not equivalent to generalization, it appears highly correlated with LLMs’ reasoning capabilities. This work provides a brief overview of the underlying theory and a limited set of experiments, suggesting that further exploration of these phenomena could be key to enhancing LLMs’ reasoning abilities. The researchers hope this approach may help smaller LLMs bridge the performance gap with larger models in the future.
Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter.
Join our Telegram Channel and LinkedIn Group.
If you like our work, you will love our newsletter..
Don’t Forget to join our 46k+ ML SubReddit
If You are interested in a promotional partnership (content/ad/newsletter), please fill out this form.
The post This AI Research from Tenyx Explore the Reasoning Abilities of Large Language Models (LLMs) Through Their Geometrical Understanding appeared first on MarkTechPost.