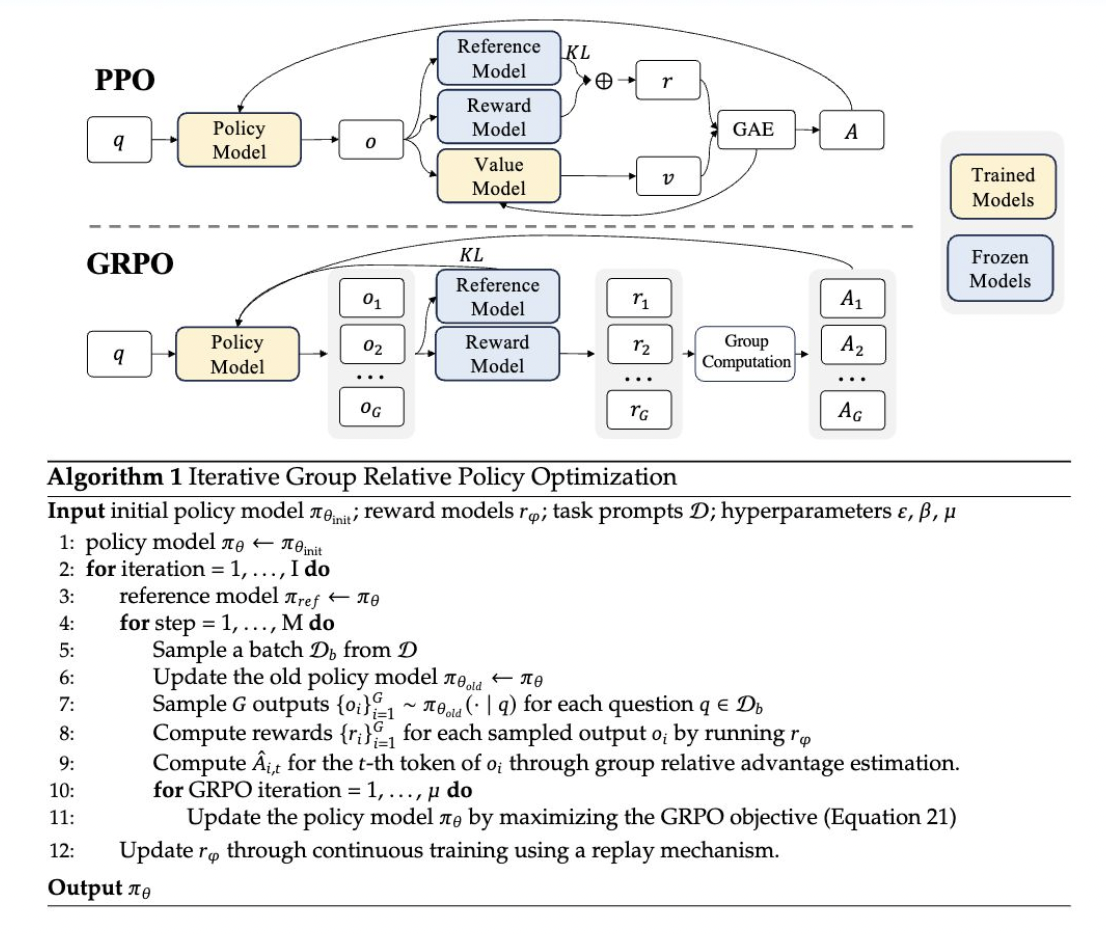

Group Relative Policy Optimization (GRPO) is a novel reinforcement learning method introduced in the DeepSeekMath paper earlier this year. GRPO builds upon the Proximal Policy Optimization (PPO) framework, designed to improve mathematical reasoning capabilities while reducing memory consumption. This method offers several advantages, particularly suitable for tasks requiring advanced mathematical reasoning.
Implementation of GRPO
The implementation of GRPO involves several key steps:
- Generation of Outputs: The current policy generates Multiple outputs for each input question.
- Scoring Outputs: These outputs are then scored using a reward model.
- Computing Advantages: The average of these rewards is used as a baseline to compute the advantages.
- Policy Update: The policy is updated to maximize the GRPO objective, which includes the advantages and a KL divergence term.
This approach differentiates itself from traditional PPO by eliminating the need for a value function model, thereby reducing memory and computational complexity. Instead, GRPO uses group scores to estimate the baseline, simplifying the training process and resource requirements.
Insights and Benefits of GRPO
GRPO introduces several innovative features and benefits:
- Simplified Training Process: By preceding the value function model and using group scores, GRPO reduces the complexity and memory footprint typically associated with PPO. This makes the training process more efficient and scalable.
- KL Term in Loss Function: Unlike other methods, which add the KL divergence term to the reward, GRPO integrates this term directly into the loss function. This adjustment helps stabilize the training process and improve performance.
- Performance Improvements: GRPO has demonstrated significant performance improvements in mathematical benchmarks. For instance, it has improved GSM8K and the MATH dataset scores by approximately 5%, showcasing its effectiveness in enhancing mathematical reasoning.
Comparison with Other Methods
GRPO shares similarities with the Rejection Sampling Fine-Tuning (RFT) method but incorporates unique elements that set it apart. One of the critical differences is its iterative approach to training reward models. This iterative process helps fine-tune the model more effectively by continuously updating it based on the latest policy outputs.
Application and Results
GRPO was applied to DeepSeekMath, a domain-specific language model designed to excel in mathematical reasoning. The reinforcement learning data consisted of 144,000 Chain-of-Thought (CoT) prompts from a supervised fine-tuning (SFT) dataset. The reward model, trained using the “Math-Shepherd” process, was crucial in evaluating and guiding the policy updates.
The results from implementing GRPO have been promising. DeepSeekMath substantially improved in in- and out-of-domain tasks during the reinforcement learning phase. The method’s ability to boost performance without relying on a separate value function highlights its potential for broader applications in reinforcement learning scenarios.
Conclusion
Group Relative Policy Optimization (GRPO) significantly advances reinforcement learning methods tailored for mathematical reasoning. Its efficient use of resources, combined with innovative techniques for computing advantages and integrating KL divergence, positions it as a great tool for enhancing the capabilities of open language models. As demonstrated by its application in DeepSeekMath, GRPO has the potential to push the boundaries of what language models can achieve in complex, structured tasks like mathematics.
Sources
The post A Deep Dive into Group Relative Policy Optimization (GRPO) Method: Enhancing Mathematical Reasoning in Open Language Models appeared first on MarkTechPost.